机器学习之逻辑回归实现与应用

逻辑回归是一种分类方法，而并不是回归方法。

逻辑回归（Logistic Regression）是一种广泛使用的线性分类算法，主要用于二分类问题。尽管它的名字中包含“回归”二字，但它实际上是一种分类算法。逻辑回归通过预测一个事件发生的概率，来决定该事件是否发生。

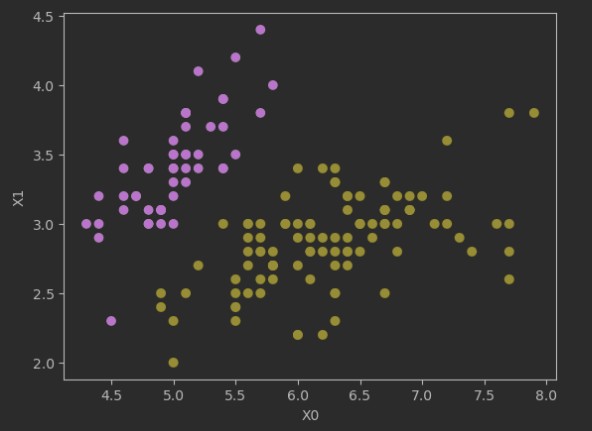
数据集： https://cdn.aibydoing.com/hands-on-ai/files/course-8-data.csv

df = pd.read_csv('./course-8-data.csv')
x = df[["X0", "X1"]].values
y = df["Y"].values
lr = 0.01  # 学习率
num_iter = 30000  # 迭代次数

model = LogisticRegression(
    tol=0.001,
    max_iter=10000,
    solver='liblinear'
)
model.fit(x,y)
# print(model.coef_,model.intercept_)

plt.scatter(df['X0'],df['X1'],c=y)
plt.xlabel('X0')
plt.ylabel('X1')

print(model.coef_.shape)
print(model.intercept_.shape)
print(x.shape)
print(y.shape)

输出如下：

(1, 2)
(1,)
(150, 2)
(150,)

import numpy as np
plt.figure(figsize=(10, 6))
plt.scatter(df["X0"], df["X1"], c=df["Y"])

x1_min, x1_max = df["X0"].min(), df["X0"].max()
x2_min, x2_max = df["X1"].min(), df["X1"].max()

xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
print(xx1.shape)
print(xx2.shape)
print(xx1.ravel().shape)
print(xx2.ravel().shape)
grid = np.c_[xx1.ravel(), xx2.ravel()]
print(grid.shape)
probs = (np.dot(grid, model.coef_.T) + model.intercept_).reshape(xx1.shape)
# 绘制等高线图
# probs = w1 * x1 + w2 * x2 + b
plt.contour(xx1, xx2, probs, levels=[0], linewidths=1, colors="red")

输出如下：

(50, 50)
(50, 50)
(2500,)
(2500,)
(2500, 2)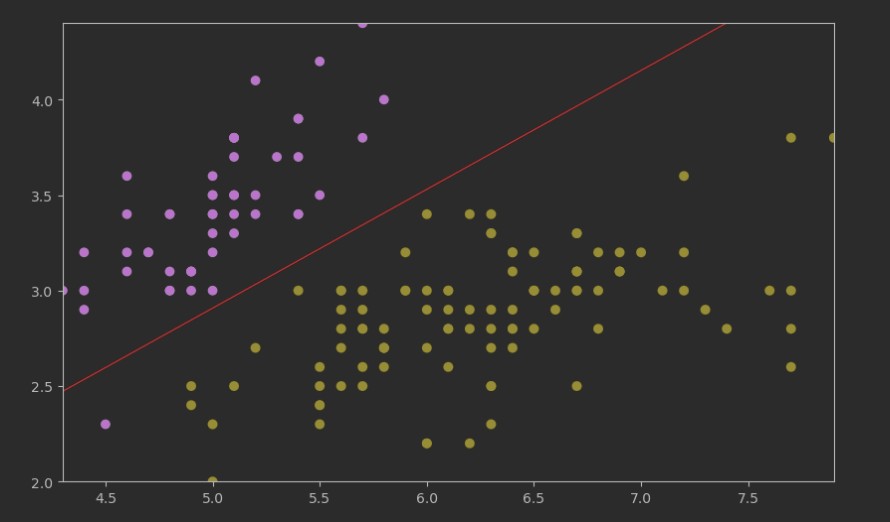

知识点

np.meshgrid

np.meshgrid是NumPy库中的一个函数，它用于生成坐标网格。在多维空间中，当你需要对一个区域进行网格化，以便进行计算或绘图时，np.meshgrid非常有用。

具体来说，np.meshgrid可以接收两个一维数组，分别表示x轴和y轴的坐标点，并返回两个二维数组，这两个二维数组的行和列分别对应输入数组的坐标点。这样，你可以很容易地对这些坐标点进行矩阵运算或在这些点上进行函数评估。

下面是np.meshgrid的基本用法：

import numpy as np

x = np.array([1, 2, 3])
y = np.array([4, 5, 6, 7])

X, Y = np.meshgrid(x, y)

在这个例子中，X和Y将是这样的二维数组：

X = [[1, 2, 3],
     [1, 2, 3],
     [1, 2, 3],
     [1, 2, 3]]

Y = [[4, 4, 4],
     [5, 5, 5],
     [6, 6, 6],
     [7, 7, 7]]

这样，X[i, j]和Y[i, j]就代表了网格中的一个点，其中i是行索引，j是列索引。

np.meshgrid函数还有几个可选参数，例如：

• indexing：默认值为'xy'，表示第一个参数对应x轴，第二个参数对应y轴。如果设置为'ij'，则表示第一个参数对应行索引，第二个参数对应列索引。
• sparse：默认为False，如果设置为True，则返回稀疏数组，这在处理大型网格时可以节省内存。

np.meshgrid在科学计算和数据可视化中非常常见，特别是在需要对函数进行二维或多维插值、计算或绘制图形时。

np.c_

np.c_ 是 NumPy 库中的一个函数，用于沿着列方向（即沿着第二个轴）堆叠数组。它是用于列向量或列矩阵的堆叠的快捷方式。当你想要将多个数组并排放置，形成一个新的二维数组时，可以使用 np.c_。

np.c_ 的使用示例如下：

import numpy as np

# 创建两个一维数组
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

# 使用 np.c_ 将数组 a 和 b 沿着列方向堆叠
c = np.c_[a, b]

执行上述代码后，c 将变成：

array([[1, 4],
       [2, 5],
       [3, 6]])

这里，np.c_[a, b] 等价于 np.column_stack((a, b))，np.column_stack 函数是 np.c_ 的等效函数，用于将多个一维数组或列向量堆叠成一个二维数组。

np.c_ 也可以用于堆叠更多的数组，例如：

d = np.array([7, 8, 9])
e = np.c_[a, b, d]  # 将 a, b, d 堆叠成列

这将得到：

array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

np.c_ 通常用于数据预处理或在进行矩阵运算时需要将多个数组组合成一个矩阵的场景。

.ravel()方法

在NumPy中，.ravel()方法用于将多维数组（ndarray）降维成一维数组。如果数组已经是一维的，.ravel()方法将返回其自身的视图。如果数组是多维的，.ravel()会返回数组的一维副本，但不会改变原始数组的形状。

使用.ravel()方法时，可以指定一个可选的order参数，它控制数组的展开顺序。默认情况下，order参数是'C'，表示按C语言的行优先顺序展开数组。如果设置为'F'或'A'，则会按列优先顺序（即Fortran顺序）展开数组。

下面是.ravel()方法的使用示例：

import numpy as np

# 创建一个二维数组
a = np.array([[1, 2, 3], [4, 5, 6]])

# 使用 ravel() 将数组降维成一维数组
b = a.ravel()

print(b)  # 输出: [1 2 3 4 5 6]

# 如果数组已经是一维的，ravel() 将返回其自身的视图
c = np.array([1, 2, 3, 4, 5, 6])
d = c.ravel()

print(d is c)  # 输出: True，表示 d 和 c 是同一个对象

使用order='F'参数时：

# 创建一个二维数组
e = np.array([[1, 2, 3], [4, 5, 6]])

# 使用 ravel() 并指定 order='F' 按列优先顺序展开数组
f = e.ravel(order='F')

print(f)  # 输出: [1 4 2 5 3 6]

.ravel()方法在需要将多维数组转换为一维数组进行操作时非常有用，例如在机器学习算法中对特征向量进行处理。

plt.contour

plt.contour 是 Matplotlib 库中的一个函数，用于绘制等高线图（contour plot），这种图表可以展示数据的三维形状在二维平面上的投影。

等高线图通常用于表示一个二维区域内的数值变化，例如地形图、温度分布图或任何二维函数的等值线图。在机器学习中，等高线图常用于可视化决策边界。

下面是 plt.contour 函数的一些常用参数及其作用：

• X 和 Y: 这两个参数是可选的，它们分别代表数据点的 x 轴和 y 轴坐标网格。如果提供了 X 和 Y，则 Z 参数必须是一个与 X 和 Y 形状相同的二维数组。如果没有提供 X 和 Y，则 Z 必须是二维数组，并且 plt.contour 会隐式地使用 Z 的行索引和列索引作为坐标。

• Z: 这是一个二维数组，包含了要绘制的数值数据。等高线图将展示这些数值的等值线。

• levels: 这个参数定义了要绘制的等值线的具体数值。如果未指定，plt.contour 将自动选择等值线的数量和位置。如果指定为一个数组，将绘制数组中定义的特定等值线。

• linewidths: 这个参数控制等高线的宽度。它可以是一个数值，表示所有等高线使用相同的线宽，或者是一个与 levels 数量相同的数组，表示每条等高线的具体线宽。

• colors: 这个参数定义了等高线的颜色。它可以是一个颜色名称、十六进制颜色代码，或者是一个颜色映射表的名称。

• alpha: 这个参数控制等高线的透明度。

• label: 用于图例的标签。

• norm: 一个归一化对象，它将 Z 中的值映射到 colors 参数指定的颜色。

• extent: 用于指定 X 和 Y 轴的范围，如果没有提供 X 和 Y，则这个参数特别有用。

• transform: 用于指定坐标轴的变换。

等高线图的绘制通常需要三个主要步骤：

1. 准备数值数据（Z）。
2. 使用 np.meshgrid 生成坐标网格（如果需要）。
3. 调用 plt.contour 绘制等高线。

例如：

import matplotlib.pyplot as plt
import numpy as np

# 创建数据
x = np.linspace(-3.0, 3.0, 100)
y = np.linspace(-3.0, 3.0, 100)
X, Y = np.meshgrid(x, y)
Z = np.sin(X) * np.cos(Y)

# 绘制等高线图
plt.contour(X, Y, Z, levels=14, linewidths=1, colors='red')
plt.colorbar()  # 显示颜色条
plt.show()